Post-Quantum Signature Schemes from Oneway Functions
PICNIC [1] belongs to a wider class of signature schemes where the secret key is an input to a oneway function, and the public key is the output. This low level requirement allows to reuse presumed quantum-resistant symmetric primitives.
For instance, the oneway function used in PICNIC is built from a traditional block cipher and transforms a random plaintext and key (which together make up the secret key) into a plaintext and ciphertext (the public key) by encryption (Figure 1). This is a oneway function for many block ciphers because a full inversion requires a key recovery.
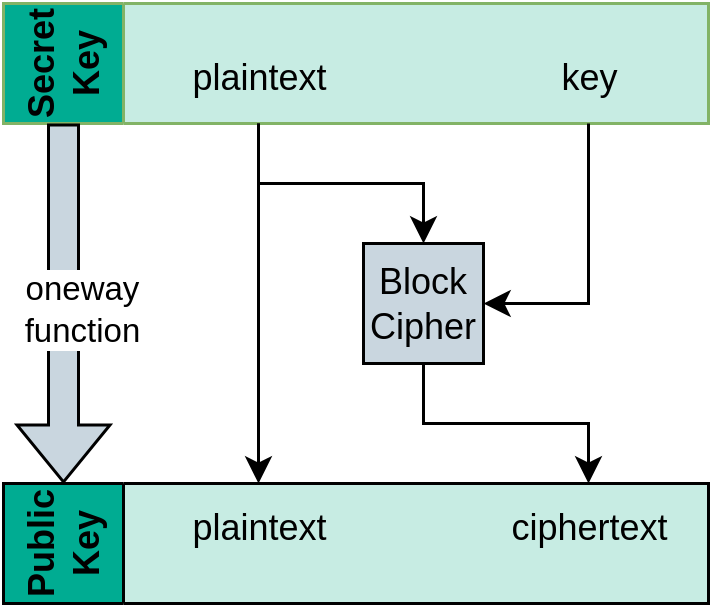
Figure 1: Generation of a secret key and a public key using a block cipher. The secret key is the plaintext and the encryption key, the public key is the plaintext and the ciphertext.
There are two predominant techniques to create signatures from arbitrary oneway functions. Well known are Lamport and Merkle Signatures, which form the basis of Hash-based signature schemes. In constrast, MPCitH [2] signatures use a much more flexible construction based on proofs of knowledge.
Signatures and Proofs of Knowledge
To understand this connection of oneway functions to signature schemes, we need to understand a particular zero knowledge proof of knowledge. Assume that someone (whom we call the prover) wants to convince to you (the verifier) that they know of a secret key for a given public key. They could do that as follows:
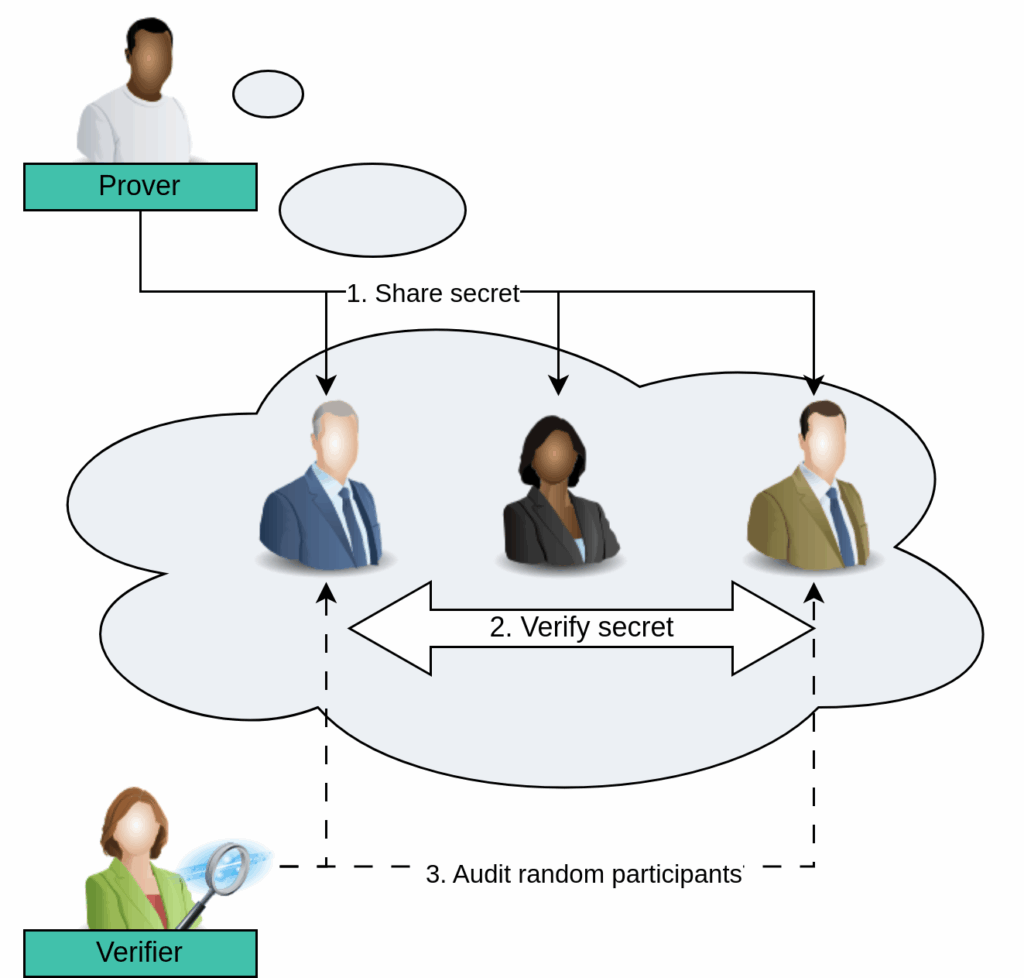
Figure 2: The prover splits his secret on different parties. These parties evaluate a public function, without learning the secret of the other parties. The verifier checks all except one party to verify consistency within these parties.
The prover splits the secret key into »key shares«. These are random looking values which XORed together would yield the secret key again. Given all shares, one can recover the secret key, but even missing one share, one gains no information about it. The prover gives each share to one of their friends.
The friends use the protocol below to assess whether the XOR of their shares really is the secret key corresponding to the public key. They make sure that no friend by themselves learns anything about the secret key.
Each friend sends a salted hash of their inputs to the verifier. The verifier then chooses a random subset of friends to reveal all their inputs and salt. The verifier checks that the received values really belong to the salted hashes and that that the friend rightfully concluded that the XOR of all shares was a valid preimage, according to the protocol.
If the prover really knows a preimage and the friends are following the protocol, then no auditing by the verifier will ever fail. If the prover does not know a preimage, then the checking protocol can only succeed if at least one friend is not following the protocol. If that friend is randomly chosen to be audited, the verifier will notice. Thus, if after many repetitions of the above three steps the verifier does not find a cheating friend, the verifier can conclude that the prover really knows the secret key.
MPC-in-the-Head signatures exploit these three steps to derive signatures. The signer simulates the actions of all friends »in their head«, and pick the parties to disclose by hashing the salted hashes and the message to sign. The signature itself (barring any optimizations) consists of the salted hashes and revealed values. To verify a signature, the verifier once again hashes the salted hashes and the message, makes sure that the correct friends have disclosed their values, and audits them like in step 3 above. This procedure binds the proof to a message: To sign a different message, you need to create a new proof and reveal different friends’ inputs.
A Basic Share Checking Protocol
How can the friends check whether their shares would combine to a preimage of the public key, without any friend learning the secret key? The answer lies in a field called Multi-Party-Computation (MPC). Let us sketch such a protocol for three friends.
Consider an electronic circuit computing the oneway function consisting only of AND and NOT gates (any function can be represented in this way). The circuit has an input wire for each bit of the secret key, an output wire for each bit of the public key, and several intermediate wires (Figure 3).
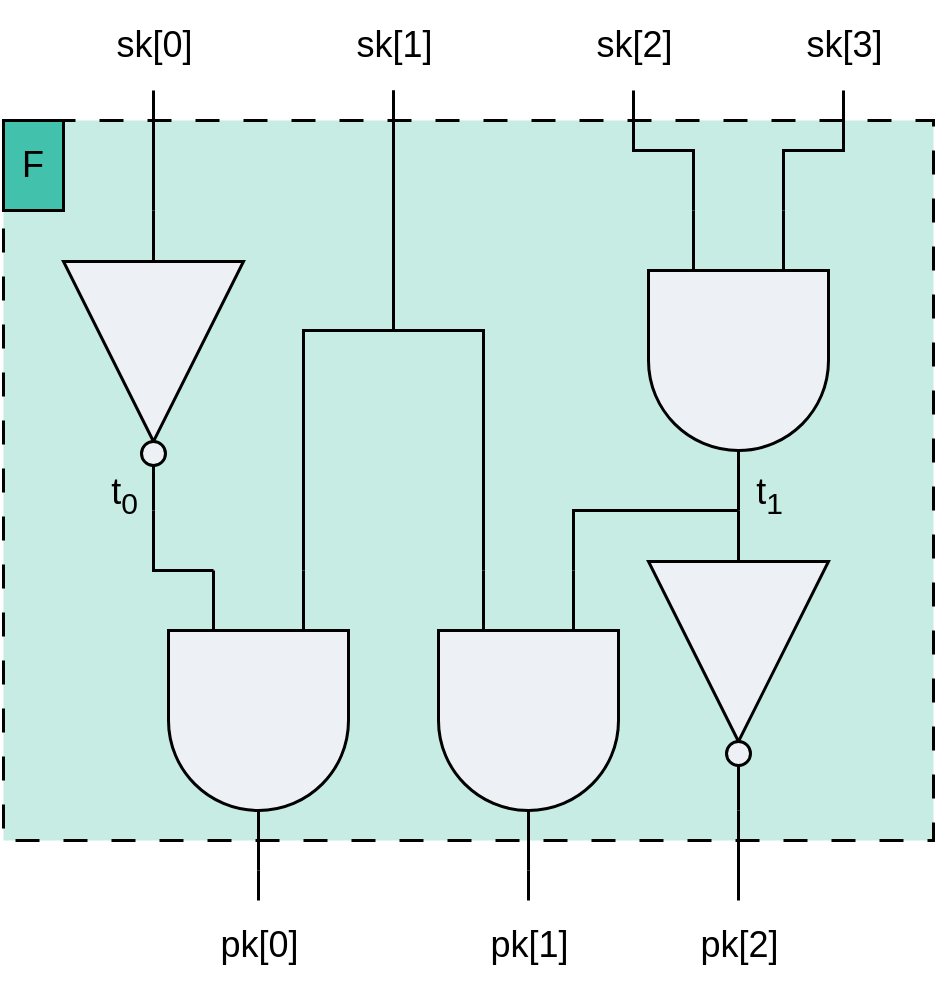
Figure 3: An example circuit consisting of NOT and AND gates. The circuit gets four bit secret key (sk) as input and outputs a three bit public key (pk).
Before the checking protocol, each friend has a share for each input wire. The parties can work together to obtain shares for each intermediate and output wire. Finally, they combine their shares for each output wire and check whether the results are the public key bits.
When encountering a NOT gate, the first two friends take the output share to be the same as the input share, the third friend takes their output share to be the opposite of the input share (Figure 4). (Thus, the XOR of all output shares is NOT the XOR of all input shares.)
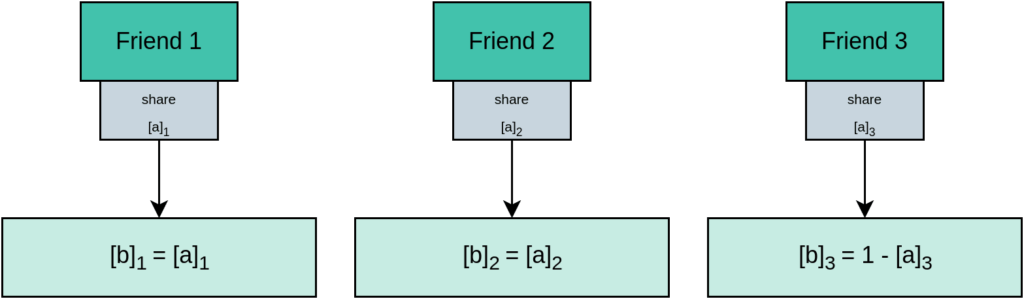
Figure 4: MPC computation of a NOT gate.
For an AND gate, each friend generates an additional bit, and sends it clockwise to the next friend, along with their input shares to the gate. Now, each party calculates the output share according to the formulas below. Again, this computation ensures that the XOR of all output shares is the AND of the XORs of the input shares. The additional bit ensures that information flowing from friend 1 to friend 2 is masked before flowing to friend 3 at the next AND gate (Figure 5). (Otherwise friend 3 would have information from all three friends and could potentially recover secrets).
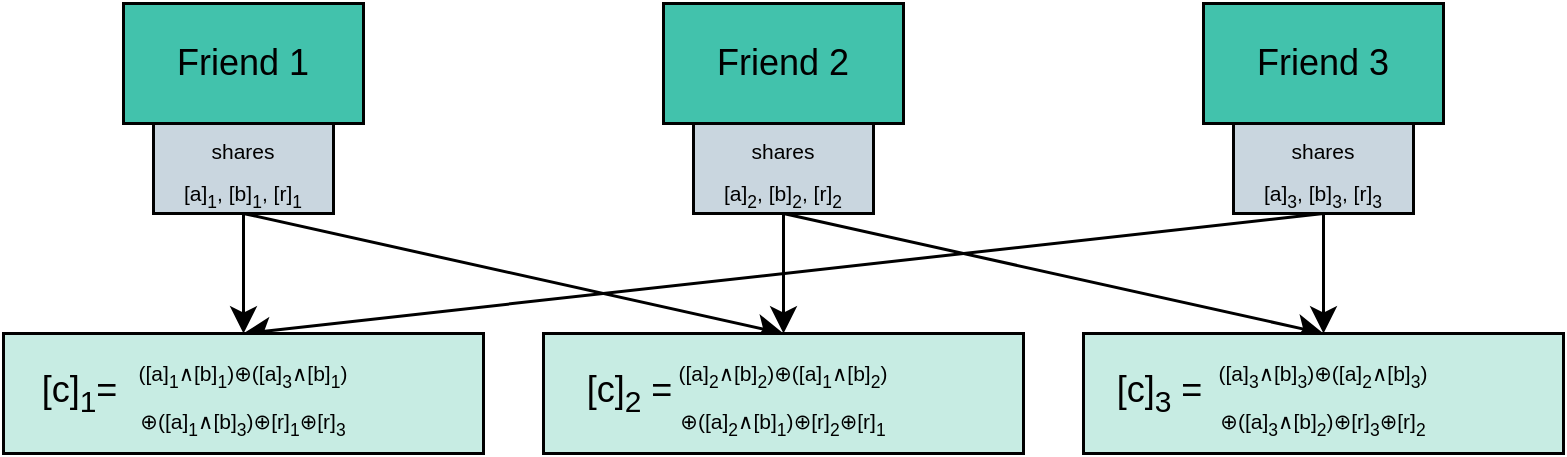
Figure 5: MPC computation of an AND gate.
Throughout this entire process, no single friend learns anything about the actual value of any non-output wire. Thus, the verifier can safely inspect one friend and all shares received by that friend.
Why is the MPC-in-the-Head paradigm of such interest?
The great advantage of the PICNIC framework is that its security only depends on the used block cipher and hash function, rather than e.g. some more structured number theoretic assumption. In other schemes, advances in the math behind these assumptions might eventually be exploited to break the scheme. Additionally, the block cipher can be exchanged arbitrarily. In the original PICNIC, the LowMC [3] block cipher was used, as it is optimized for MPC computation, leading to sufficiently small signatures. In follow-up work, the AES [4] block cipher was utilized. Here, signatures could be made sufficiently small by improving the underlying MPCitH proof protocol.
Another significant advantage of signatures based on the PICNIC framework is their small keys. Since key generation is done with a block cipher, the public key is 32 bytes, and the secret key is only 32 bytes. This is very small compared to other post-quantum signature algorithms.
Where does Fraunhofer AISEC use the MPCitH paradigm?
The anonymity network TOR [5] and the GNU Name System (GNS) [6] depend on a technique called key blinding. These systems rely on key blinding to maintain user anonymity and privacy, as well as to ensure censorship resistance. Key blinding is a cryptographic method that enhances user privacy by ensuring that the public key used in verification (called the blinded public key) remains unlinkable to the original public key. This can be done trivially for classical signature schemes but is ongoing research question for post-quantum signature schemes.
Eaton et al. [7] suggested an approach on how PICNIC could be used to solve the key blinding issue, which is, as they pointed out, insecure against a Meet-in-the-middle attack. We aim to enhansce the user anonymity and privacy, so currently, we are building a key blinding framework based on their idea while maintaining the MPCitH approach. Additionally, we provide an implementation for this framework and aim to integrate it into GNS [8]. Here, the small keys are particularly useful.
Glossary of terms
primitives: Cryptographic schemes and protocols are often composed from individually auditable primitives, e.g. AES256, RSA, SHA256
block cipher: A keyed random looking permutation. Examples include AES256 or DES.
key recovery: A form of attack aiming to recover the secret key used for a primitive.
XOR: A mathematical operation efficiently performed by computers.
oneway function: A function for which a random input can not be found given just the corresponding output.
preimage: A function input corresponding to a given function output.
TOR: Short for »The Onion Router«. A project aimed at circumventing censorship and providing anonymity, a prerequisite e.g. for free journalism in authoritarian states.
Bibliography
[1] Chase, Melissa and Derler, David and Goldfeder, Steven and Katz, Jonathan and Kolesnikov, Vladimir and Orlandi, Claudio and Ramacher, Sebastian and Rechberger, Christian and Slamanig, Daniel and Wang, Xiao and others, “The picnic signature scheme,” Submission to NIST Post-Quantum Cryptography project, 2020.
[2] Ishai, Yuval and Kushilevitz, Eyal and Ostrovsky, Rafail and Sahai, Amit, “Zero- knowledge from secure multiparty computation,” in Proceedings of the thirty-ninth annual ACM symposium on Theory of computing, 2007, pp. 21–30.
[3] Albrecht, Martin R and Rechberger, Christian and Schneider, Thomas and Tiessen, Tyge and Zohner, Michael, “Ciphers for MPC and FHE,” in Advances in Cryptology– EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, April 26-30, 2015, Proceedings, Part I 34, 2015, pp. 430–454.
[4] Joan, Daemen and Vincent, Rijmen, “The design of Rijndael: AES-the advanced encryption standard,” Information Security and Cryptography, 2002.
[5] Dingledine, Roger and Mathewson, Nick and Syverson, Paul F and others, “Tor: The second-generation onion router.,” in USENIX security symposium, 2004, pp. 303– 320.
[6] Schanzenbach, Martin and Grothoff, Christian and Fix, Bernd, “The GNU Name System,” in RFC Series 9498, vol. 9498, RFC Editor, 2023.
[7] Eaton, Edward and Stebila, Douglas and Stracovsky, Roy, “Post-quantum key- blinding for authentication in anonymity networks,” in Progress in Cryptology– LATINCRYPT 2021: 7th International Conference on Cryptology and Information Security in Latin America, Bogot{‘a}, Colombia, October 6–8, 2021, Proceedings 7, 2021, pp. 67–87.
[8] Martin Schanzenbach and Christian Grothoff and Bernd Fix, RFC 9498: The GNU Name System, RFC Editor, 2023.
Authors

Thomas Bellebaum
Thomas Bellebaum has been a research associate in the field of Applied Privacy Technologies at the Fraunhofer Institute for Applied and Integrated Security (AISEC) since 2021. His areas of interest include advanced cryptographic methods such as secure data re-encryption (Proxy Re-encryption) and key derivation (Key Blinding), as well as post-quantum encryption methods. He received his Master of Science in Computer Science from the Technical University of Munich.
Contact: thomas.bellebaum@aisec.fraunhofer.de

Markus Bever
Markus Bever has been working in the Applied Privacy Technologies department at Fraunhofer AISEC since 2025. He specializes in the field of cryptography, focusing on the integration of post-quantum cryptography into various applications. Markus received his Master of Science in Computer Science from the Technical University of Munich.
Contact: markus.bever@aisec.fraunhofer.de








