Software testing is a critical part of the software development lifecycle, ensuring the reliability, security, and functionality of software systems. Effective software verification and validation can lead to significant cost savings, especially when applied early in development. By identifying and fixing flaws before they propagate into later stages or deployed systems, organizations can avoid excessive costs and reputational damage.
Formal verification methods utilize mathematical models to confirm the correctness of software against specified behaviors. For instance, in a banking transaction system, one might specify that an account balance should never become negative. Various techniques exist to build abstract models from source code and specifications, such as symbolic execution and control flow graph analysis.
However, formal verification has its challenges. Rice’s theorem [1] asserts that if a property does not hold for all programs, no algorithm can correctly decide its validity across all possible programs. This restricts the properties we can certify. Additionally, many verification problems are NP-hard, therefore at least as hard as all the problems that can be efficiently verified and strongly believed to be computationally intensive. Here, quantum computing may provide more efficient solutions to these complex problems.
Our Approach
Our research presents an end-to-end pipeline for verifying software using quantum algorithms:
- Property Specification: Define properties to be verified in the code.
- SAT Formula Generation: Create a SAT formula that indicates whether a problematic input exists.
- Optimization Problem Formulation: Transform the SAT formula into a Quadratic Unconstrained Binary Optimization (QUBO) problem.
- Quantum Solution: Utilize quantum devices to solve the optimization problem.
Generating a SAT Instance
Formally verifying software means proving that certain defined properties hold for every possible input. Typical properties include preventing buffer overflows and ensuring function outputs are within valid ranges.
The process for generating a SAT Instance generally follows a structured approach:
- Control Flow Graph (CFG) Construction: A CFG is created to model the program’s flow, representing all possible paths that execution can take through the code. Every path corresponds to a possible computation. Once the CFG has been created, it must be determined whether there are any problematic paths.
- Property Encoding: The properties to verify are identified and encoded as “good” and “bad” states in the CFG. For example, if we want to ensure that a variable does not exceed a certain boundary, we represent this concern in the graph. If a path now ends in a bad state, we consider the path bad.
- Path Extraction: The CFG is analyzed to extract all paths leading to undesirable states, which are then represented as logical clauses. The analysis must examine how a bad state can be reached, than identify any states that can lead to a bad state, and so on. If this approach finally leads to the entry point of the program, it means that there will also be a path to the bad state.
- Logical Formula Construction: These paths are expressed in Conjunctive Normal Form (CNF), where each path corresponds to a clause. A clause is satisfied if at least one of its literals is true, indicating that an undesirable condition can occur.
By following these steps, a SAT formula is generated that is satisfiable if the program contains a flaw. This method allows for the systematic conversion of code logic into a format suitable for verification.
This conversion from C code to SAT instances can be performed using existing tools, such as CBMC, which automatically generates SAT instances based on specified errors. The resulting SAT formula can be further processed using libraries like PySMT and Z3 for simplification, so the optimization problem becomes simpler, while still solving the same problem.
Generating the Optimization Problem
The Quadratic Unconstrained Binary Optimization (QUBO) formulation is particularly suitable for quantum computing, as it maps binary variables and objective functions into the language of qubits.
For our approach, we convert logical formulas into QUBO format, ensuring that the solution corresponds to satisfying assignments.
Finding the Optimum
We explored three kinds of quantum algorithms to find optimal solutions:
- Variational Quantum Algorithms (VQA): We used the Variational Quantum Eigensolver (VQE) and Quantum Approximation Optimization Algorithm (QAOA), which showed promise in converging to optimal solutions. VQA methods are adaptable and used to optimize parameters iteratively to minimize a given cost function, often resulting in faster convergence.
- Grover’s Algorithm: This approach utilizes Grover amplification; however, our experiments revealed that noise in quantum hardware significantly impacted results, leading to mostly random outputs. Grover’s algorithm provides a quadratic speedup for unstructured search problems, but its effectiveness can diminish in noisy environments.
- Quantum Singular Value Transformation (QSVT): This technique applies a polynomial to the singular values of matrices, filtering out non-solutions. Although theoretically robust, practical implementation faced challenges, particularly with block encoding.
- Non-solutions are filtered: The polynomial filter function is designed so that only valid solutions (i.e., assignments satisfying the SAT instance) are amplified, while non-solutions are suppressed, some approximations of different degrees can be seen in Figure 1. This selective amplification is critical for identifying correct program behaviors.
- The suppression of non-solutions leads to a bandpass: The filtering function effectively acts like a bandpass, allowing only a range of values to pass and removing all others, sharply distinguishing between solutions (which are passed/amplified) and non-solutions (which are blocked/suppressed).
- The optimal version of this function cannot be a polynomial, since it is not continuous: Ideally, the filter would be a perfect step function, but such a function is discontinuous and cannot be represented exactly by a polynomial. Therefore, QSVT must approximate this behavior using high-degree polynomials.
- The required precision of the approximation depends on the gap: the smaller the gap, the higher the necessary degree — and, consequently, the longer the execution time: The quality of the polynomial approximation is crucial. If the spectral gap between solutions and non-solutions is small, a higher-degree polynomial is needed for sharp separation, which increases the computational resources and execution time required. This is colorfully depicted in Figure 2.
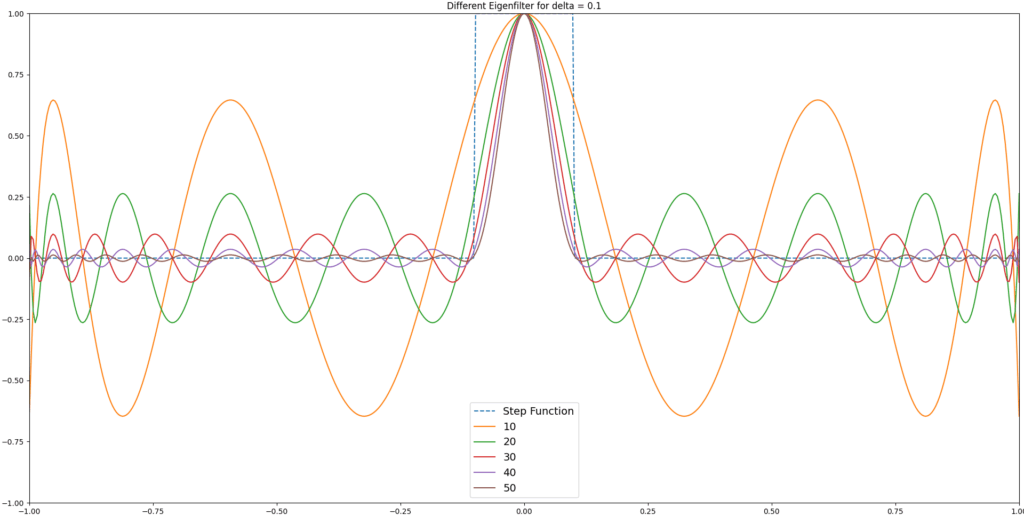
Figure 1: Different approximations of the step function.
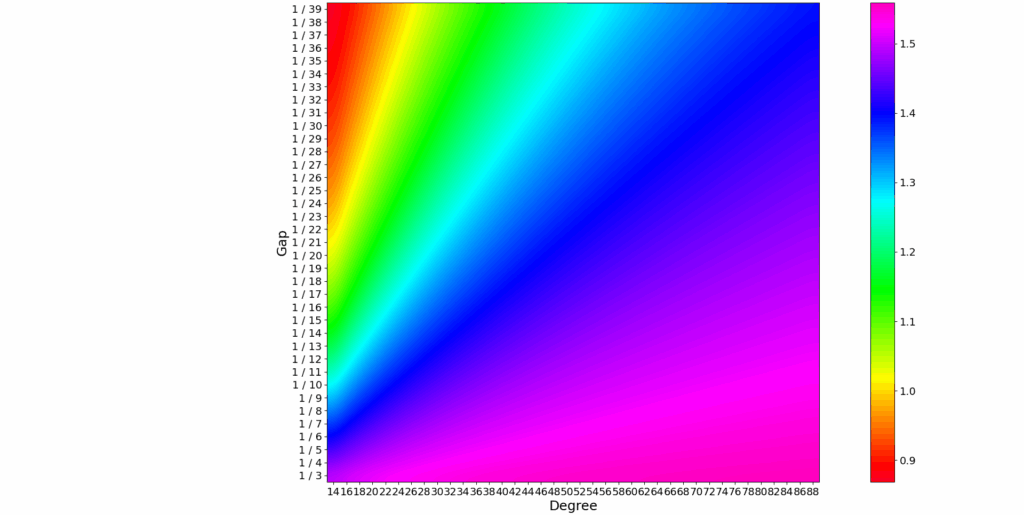
Figure 2: How strong solutions are amplified, compared to non-solutions.
Random Access Coding
An interesting technique we explored is Random Access Coding (RAC). This method allows for the encoding of multiple variables into a single qubit, potentially reducing the required memory by up to a factor of three. In practice, however, this factor tends to be closer to 2.5 due to the overhead of additional iterations required to extract the needed information.
RAC works by encoding multiple bits of information into a single quantum bit (qubit), allowing us to extract multiple variables from fewer measurements. The key abstraction is that while we can encode up to three variables within one qubit, we can only reliably extract one variable at a time with a certain probability (approximately 0.79). This leads to a trade-off where we need more iterations to achieve a solution, but it also enables the solving of larger problems that might be infeasible otherwise.
When using RAC within the framework of Random Access Optimization (RAO), the solutions of the old and new problems relate as follows: the new problem, which utilizes RAC, may require more iterations to converge to a satisfactory solution, but it operates on a reduced memory footprint. This allows for the tackling of problems that would otherwise exceed the limitations of the quantum hardware, at the cost of longer computation than would be necessary without the coding.
It can be used with most of the other methods and is a nice tool to have should a problem turn out to need more memory than available.
Experimental Setup
We conducted experiments using a 27-qubit IBM Quantum System One and later the 127-qubit ibmq_nazca system. Our test cases included both common programming errors and synthetic instances designed to validate our approach.
Results Overview
Our findings indicated that VQA, particularly QAOA with the COBYLA optimizer, achieved the fastest convergence. However, as the complexity of problems increased, so did the number of required iterations. Grover’s performance on actual hardware was less favorable, with most outputs resembling random results due to noise interference.
Test Cases
We selected various programming errors and logical expressions for testing, summarized in Table I. These examples were intentionally chosen to be small yet interesting, as they cover fundamental logic, arithmetic, and memory-related problems. The minimalistic nature of these examples makes them ideal for demonstrating common issues in software while remaining manageable for quantum verification techniques.
Name | Test Case |
Out of Bounds | int buf[1]; buf[1] = 0; |
Invalid Conversion | short s = 1024; char c = (char)s; |
Division by Zero | float i = 1 / 0; |
Memory Leak | void *p = malloc(1); p = 0; |
Not a Number | float i = 0.0 / 0.0; |
Overflow | int k = 0x7FFFFFFF; k += 1; |
Null-Pointer Dereferencing | int *p = 0; int i = *p; |
Addition | a + b = 2c + d |
Program Flow | (a = b = c) ∧ (d + e + f > 1) |
Indicator | 2a + b > 2c + d |
OR | ∧_{j=1}^n x_j |
XOR | ⊕_{j=1}^n x_j |
Unique | ∑_{j=0}^5 2^j x_j ∈ {42} |
Two-Solutions | ∑_{j=0}^{13} 2^j x_j ∈ {15, 240} |
Three-Solutions | ∑_{j=0}^7 2^j x_j ∈ {42, 101, 205} |
These examples represent minimal instances of common programming errors and logic problems. Their simplicity allows for focused experimentation, while their varied nature ensures a comprehensive assessment of the verification techniques.
Conclusion
Our research illustrates that using quantum computing for software verification is feasible and holds significant promise for improving efficiency in identifying programming errors. While current quantum devices present challenges, advancements in quantum technology may yield better solutions in the future.
Future Directions
Looking ahead, research can explore various avenues to enhance this approach, including:
- Experimenting with different encoding strategies to optimize for specific quantum hardware.
- Investigating hybrid models that combine classical and quantum techniques.
- Enhancing block encoding methods to improve QSVT applications on quantum hardware.
As quantum computing continues to advance, the intersection with software verification promises to be a dynamic field rich with exploration opportunities.
References
The references used in this research can be found in our paper »Towards Classical Software Verification using Quantum Computers«[2] covering foundational concepts in software verification, quantum algorithms, and related tools.
[1] Rice, H. G. (1953). Classes of recursively enumerable sets and their decision problems. Transactions of the American Mathematical Society, 74(2), 358–366. https://doi.org/10.1090/S0002-9947-1953-0053041-6
[2] S. Issel, K. Tscharke and P. Debus, “Towards Classical Software Verification using Quantum Computers,” 2025 International Conference on Quantum Communications, Networking, and Computing (QCNC), Nara, Japan, 2025, pp. 598-605, doi: 10.1109/QCNC64685.2025.00099
Author

Sebastian Issel
Sebastian Issel is a researcher at Fraunhofer Institute for Applied and Integrated Security AISEC in the Quantum Security Technologies group. His research focuses on quantum computing, in particular applications of the quantum singular value transformation and optimization.








